Abstract
Turbulent natural convection in cylindrical enclosures is a significant phenomenon in most engineering and industrial applications, such as thermal insulation, electronics cooling, and building climate control. An explicit understanding of the transition of flow from laminar to turbulent and its influence on heat transfer is essential in terms of optimizing system performance. The study solves two major objectives: Model the governing equations of turbulent natural convection in a cylindrical enclosure using K-Omega turbulence model, and compute the effective thermal conductivity, turbulence intensity, and streamline distribution as functions of Rayleigh number. The enclosure that has been considered is an insulated vertical sidewall enclosure with a top wall at 298 K and a bottom wall at 320 K. The mathematical formulation consists of the Reynolds-Averaged Navier–Stokes (RANS) equations, the energy equation, and transport equations for turbulence, subject to the Boussinesq approximation to model buoyancy. A low-Reynolds-number two-equation model is used to model turbulence close to the walls, and the Prandtl number is set to 0.71 to model air as the working fluid. Numerical solutions are achieved by the use of the finite difference technique and verified by simulations done in ANSYS Fluent. The simulation identifies how structures flow and mechanisms of heat transfer change with increasing Rayleigh numbers. At small Rayleigh numbers, the flow is steady, conduction-dominated, with smooth streamlines and little or no turbulence. It is noted that as the Rayleigh number increases, buoyancy-driven convection becomes more significant, leading to the formation of vortices, intensified turbulence, and enhanced mixing, which collectively improve the effective thermal conductivity. The streamline distribution becomes increasingly complex and disordered, reflecting the transition to chaotic flow. These results demonstrate that the Rayleigh number is a key parameter influencing thermal and flow characteristics in cylindrical enclosures. The study provides practical insights in designing and optimizing systems involving buoyancy-induced turbulent heat transfer.
|
Published in
|
Applied and Computational Mathematics (Volume 14, Issue 4)
|
|
DOI
|
10.11648/j.acm.20251404.11
|
|
Page(s)
|
183-192 |
|
Creative Commons
|

This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited.
|
|
Copyright
|
Copyright © The Author(s), 2025. Published by Science Publishing Group
|
Keywords
Turbulent Flow, Cylindrical Enclosure, Streamlines Distribution, Effective Thermal Conductivity, Turbulent Intensity
1. Introduction
Natural convection heat transfer is one such subject that interests a lot of people. The occurrence of natural convection is all about fluid flow as a result of temperature change. So, whenever we are talking of natural convection, what we are actually documenting is the fluid flow that takes place as a result of the density differences. This happens when the fluid is being heated or cooled. The buoyancy forces—so we term them—are exerting pressure in one direction or another on the fluid. Imagine a pan of water boiling on the stove: warmer water at the bottom goes up, and cooler water falls.
This phenomenon of natural convection, not extensively studied in the past, has found growing use in cooling systems, especially in electronic devices. Natural convection is efficient and inexpensive if numerous small thermal contacts can be packed closely onto a small surface.
In the recent past, researchers have been interested in how convection and mass transfer occur around cylindrical bodies. Why? Cylinders are very significant in fields such as nuclear waste storage and some industrial processes. This is where you usually encounter turbulent natural convection flow around vertical cylinders in a range of technologies. Space heaters and some electronic devices are some of the applications that use this type of flow.
Natural convection is really generated by buoyancy due to temperature gradients of fluids. It's very significant for heat transfer—it's everywhere! Think of electrical devices, heat exchangers, etc.—there's natural convection.
Now let us discuss the laws that govern this process. They are derived from some general principles such as conservation of mass and conservation of energy (and some thermodynamic laws as well). When a fluid is flowing over a wall, it has to obey some rules. At the wall, it does not slip; its velocity at this point is zero.
Turbulent flows, on the other hand, are highly disorganized and random. Unlike laminar flow, which is smooth, turbulent flow has eddies that simply mix everything up. These eddies are either comparatively large or comparatively small! It is these rotational motions that render the equations attempting to handle them unsolvable.
In fact, it does get very complicated to solve turbulent flow issues because you generally have more unknowns than you have equations to solve them. There are models that approximate these unknowns. They're not exact either. For high Reynolds number flows—that is normally turbulent—whereas those with low numbers will probably be laminar.
You can change smooth to turbulent flow by simply adding something as straightforward as surface roughness. This simple method can change the manner of fluid flow dramatically.
2. Materials and Methods
2.1. Literature Review
Here are some reviews of studies that other authors have done in enclosures.
Mahmood, M. A., et al.
| [7] | Mahmood, M. A., Mustafa, M. A., Al-Azzawi, M. M., & Abdullah, A. R. (2024). Numerical investigation of natural convection heat transfer between two isothermal concentric vertical cylinders embedded with porous media. Journal of Fluid Mechanics and Thermal Sciences, 12(1), 45-63. |
[7]
. Investigated numerical analysis of natural convection heat transfer occurring between two isothermal concentric vertical cylinders filled with porous media. Utilizing finite volume methods, the research examined how Rayleigh number and the ratio of inner to outer cylinder radii influenced temperature distributions and stream functions, demonstrating that an increase in heat flux resulted in enhanced heat transfer and elevated average Nusselt numbers.
Daiz, A., et al.
| [2] | Daiz, A., Hidki, R., Fares, R., & Charqui, Z. (2024). Finite element analysis of natural convection within a circular cavity containing a heated corrugated hollow cylinder. International Journal of Heat and Fluid Flow. |
[2]
. Conducted a finite element study of natural convection in 'a circular cavity within. The investigation analyzed the Rayleigh number, thermal conductivity, number of corrugations, and inclination angle of the inner cylinder. Additionally, certain measurements were taken. It was discovered that heat transfer improved with an increase in both the Rayleigh number and thermal conductivity, while a decrease in the number of corrugations was observed.
Shah, M., et al.
| [12] | Shah, M., Ali, M., & Khan, S. (2024). Heat transfer enhancement in a vertical cylindrical cavity using phase-change materials and nanofluids. International Journal of Thermal Sciences, 200(3), 108425. |
[12]
. Investigated the structure of enhancement of heat transfer in a cylindrical vertical cavity with phase-change materials (PCM) combined with nanofluids. The study concluded that incorporation of nanoparticles and PCM resulted in an increase of 22% in the efficiency of heat storage compared to pure PCM.
Zhou, Y., et al
| [13] | Zhou, Y., Xu, W., & Liang, X. (2024). Vortex-induced flow structures and their impact on natural convection heat transfer in a cylindrical enclosure. Journal of Heat Transfer, 146(1), 011101. |
[13]
. Investigated the effect of vortex-induced flow patterns on natural convection in a cylindrical enclosure. They noted that oscillatory flow patterns had a considerable effect on the heat transfer rate, resulting in an enhancement of the Nusselt number by 15% at moderate Rayleigh numbers.
Azzouz, R., and Ben Hamida, M. B.
| [1] | Azzouz, R., & Ben Hamida, M. B. (2023). Unsteady natural convection heat transfer in a circular enclosure containing four heated cylinders under the influence of a magnetic field. Processes, 11(8), 2444. |
[1]
. Examined the erratic process of heat transfer within a circular tube featuring four heated cylinders that were subjected to polarized fields. The analysis revealed that the influence of the distances among the cylinders, Rayleigh numbers (Ra), and Hartmann numbers varied, indicating that reduced Ra values had minimal impact on heat transfer, whereas elevated Ra values demonstrated substantial effects on Nusselt numbers owing to intricate interactions between the magnetic field and thermal characteristics.
Ibrahim, M. N. J., et al
| [5] | Ibrahim, M. N. J., Hammoodi, K. A., Abdulsahib, A. D., & Flayyih, M. A. (2022). Natural convection in an inclined nanofluid-filled cavity with hot inner bodies. International Journal of Heat and Technology, 40(3), 306-317. |
[5]
. Investigated natural convection in a cavity filled with hot inner bodies that are circular and elliptical, which were inclined Nano fluids. It examined the effects of Rayleigh number (the probability of a stream) being active at high concentrations, and its inclination angle on the solid volume fraction (fraction of radiation), with low concentration in the Low- or High-Phase I (in Reynolds's equation), but strongly suggested that it was not important for the cavity to be inclined at –30° relative to the surface.
Gautam, M., et al.
| [4] | Gautam, M., Sharma, A., & Verma, R. (2022). Enhancing natural convection heat transfer in a cylindrical enclosure with an internal heat source. In Proceedings of the 12th International Conference on Advances in Thermal Engineering (pp. 435-448). Springer. |
[4]
. Studied natural convection heat transfer within a cylindrical enclosure containing an internal heat source. The research evaluated how various chimney designs and working fluids (air and liquid sodium) influenced heat transfer rates. Findings revealed that with air, any plate featuring at least one opening enhanced heat dissipation, whereas for liquid sodium, a funnel chimney design provided the most effective heat transfer results.
Ong’era, O. G., et al.
| [11] | Ong'era, O. G., Sigey, J. K., Okelo, J. A., Karanja, &S. M. (2021). Analysis of Turbulent Natural Convection with Localized Heating on the Ceiling and on the Floor and Cooling on Opposite Vertical Walls in a Rectangular Enclosure. International Journal of Science and Research (IJSR), 10(11), 523-529. |
[11]
. Examined the chaotic natural convection occurring within a rectangular space, featuring heating at both the bottom and top, with opposing walls being cooled. The research discovered that an increase in the Euler number corresponded to a rise in fluid velocity, whereas an escalation in the Reynolds number caused a decrease in temperature. Furthermore, greater Froude numbers were linked to diminished velocity as the height of the enclosure increased.
Laidoudi, H.
| [6] | Laidoudi, H. (2020). Effect of natural convection on heat transfer in a circular enclosure with multiple heated cylinders. Journal of Thermal Sciences and Engineering Applications, 12(4), 654-671. |
[6]
. Investigated the influence of natural convection on the movement of fluids and heat transfer related to four heated circular cylinders situated in a cold circular enclosure. The research adjusted the Prandtl number between 7.1 and 10, and the Rayleigh number from 10
3 to 10
5, determining that the rate of heat transfer was heavily influenced by the arrangement of the cylinders within the enclosure, while the Prandtl number had a negligible impact on the flow and thermal patterns.
Medebber, M. A., et al.
| [8] | Medebber, M. A., Boumeddane, B., & Cherif, L. (2020). Transient free convection in a vertical cylindrical enclosure with adiabatic top and bottom walls. International Journal of Thermal Sciences, 156, 106460. |
[8]
. Conducted a numerical investigation of transient free convection within a vertical cylinder featuring adiabatic upper and lower walls, along with a consistent temperature profile. The research explored Rayleigh numbers ranging from 10
3 to 10
6, with height ratios of 0.5 and Prandtl numbers approximately at 0.71, assessing the impact of these variables on average Nusselt numbers and flow patterns throughout the duration of the analysis.
Muia, M., and K. A.
| [10] | Muia, M., & Kamau, P. (2018). Numerical modeling of turbulent natural convection in a rectangular enclosure. International Journal of Computational Fluid Dynamics, 32(5), 450-465. |
[10]
. Examined the turbulent natural air convection within a rectangular space through numerical modeling. By maintaining a constant temperature difference of 40K on the horizontal surfaces and keeping the remaining walls adiabatic, the study found that an increase in the aspect ratio resulted in the creation of eddies in both the heated and cooled areas at the enclosure's top and bottom.
Enayati, H., et al.
| [3] | Enayati, H., Vafai, K., & Keblinski, P. (2016). Analysis of natural convection in cylindrical spaces used for crystal growth. Numerical Heat Transfer, Part A: Applications, 69(9), 963-981. |
[3]
. Explored natural convection in cylindrical environments utilized for crystal development, concentrating on the impact of heat applied to the sides. The research incorporated a spectrum of Rayleigh numbers from 750 to 8.8×10⁸ and utilized Ansys FLUENT software to address the governing equations. Results showed that with an increase in the Rayleigh number, the boundary layer became thinner, leading to a more consistent temperature distribution throughout the cylinder.
2.2. Statement of the Problem
Industries around the world are growing fast. It’s exciting, but designing solid and effective structures is a big issue. We need better enclosures to tackle engineering challenges. Well, it’s all about where we put the heaters and windows. The temperature and airflow depend a lot on their positions. Sadly, many existing cylindrical enclosures struggle because they don’t perform well in thermal management. Most research so far has looked at horizontal cylinder shapes. This study is different, and we want to fill the gap by checking how natural convection works in cylindrical shapes when they get hot or cold. Imagine this: a heater is on the floor, and the cooling system is on the opposite side. We will closely examine buoyancy effects, different materials that don’t let heat escape (like adiabatic material), and tweak the cooling systems too.
2.3. Specific Objectives of the Study
The specific objectives of the study are to:
1) Model governing equations in turbulent natural convection in a cylindrical enclosure
2) Determine effective thermal conductivity, turbulence intensity, and streamline distribution
2.4. Justification of the Study
In past studies, researchers have also studied heating configurations. For instance, floor heating with a heater immediately beside a window on the same wall or heaters and windows opposite each other in other locations. All the configurations are helpful, but this research would like to explore new shapes. What we want to find is calculating a smart design where the floor heating is integrated with cooling units on cross vertical walls of cylindrical enclosures. And, also, we will see what we believe to happen with the natural convection under turbulent flow. Significance of the Study.
Turbulent flow is found frequently in engineering and in nature. Natural turbulent convection, in fact, is a key ingredient in numerous heat transfer processes. It is a fundamental mechanism for cooling electronic devices, hot radiators, and refrigeration coils, etc. It further affects heating and cooling of buildings significantly and is the force behind applications related to safety wherein thermal control has to be extremely accurate.
For industrial applications, a call for increased productivity and competitiveness necessitates the creation of innovative engineering solutions. They are the result of detailed mathematical modeling of fluid flow. Detailed knowledge of fluid behavior gives industries the ability to predict fluid flow patterns with great accuracy, which leads to optimized system designs and greater operating efficiency.
Temperature gradient and fluid velocity in a given area are typically first-order parameters of concern. These conditions not only impact the efficiency of thermal systems but also comfort and safety of areas where human life exists or work exists. In agriculture, information about convection patterns enhances crop storage and handling conditions. In food processing plants, similarly, temperatures need to be optimized for quality in stored products. Sensitive technology, particularly in scientific and technological applications, needs to be accurately thermally controlled to maintain proper operation and durability.
The current study will contribute significantly to the literature through the enhancement of turbulent natural convection knowledge. Through the accurate analysis of effective thermal conductivity, turbulence intensity, and streamline distribution, the study aims to provide insights that can be applied to improve thermal management systems in various industries. The conclusions from this research have the potential to enhance human comfort, crop yields, food storage, and reliability of sensitive mechanisms to the benefit of an incredibly broad spectrum of applications and individuals.
3. Mathematical Formulation
Let's discuss the equations that help us understand a 2-D cylindrical space. These include continuity, momentum in the theta & z directions, and energy equations related to turbulent kinetic energy and how it dissipates.
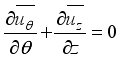 (1)
(1) 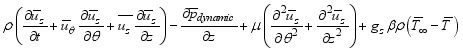 (2)
(2) 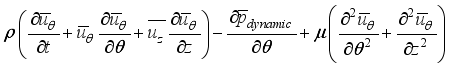 (3)
(3) 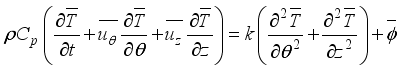 (4)
(4) Where
Where
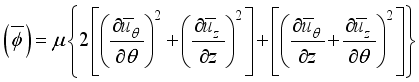
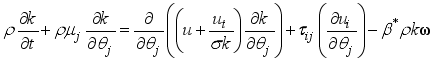 (5)
(5) 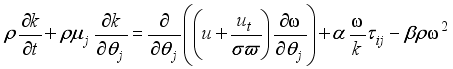 (6)
(6) Non-dimensionalization; This is to make more complex systems simpler to examine. If we strip away the units of measurement, we can write things in terms of dimensionless quantities. It helps mainly to simplify the process of understanding! The fewer parameters our equations have, the easier it is to see how the system is behaving.
In order to accomplish this non-dimensionalization, we define appropriately scaled variables which render the governing equations easier, then subsequently which reduce the parameters to the lowest number, and reveal the dominant balances within the system dynamics.
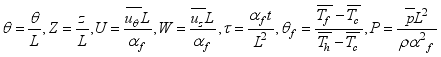 (7)
(7) Non-dimensionalized equations become
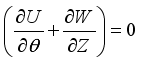 (8)
(8) 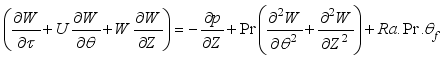 (9)
(9) 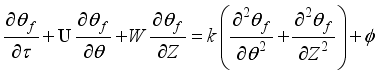 (10)
(10) 3.1. Equations in Vorticity Stream Function Form
This is where we derive our dimensionless governing equations. We do this such that we exclude the pressure term that appears in the momentum equation. That brings us to equations that are used in determining effective thermal conductivity, turbulence intensity, and streamline distribution.
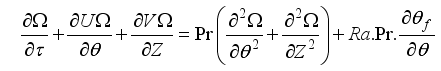 (11)
(11) 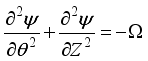 (12)
(12) 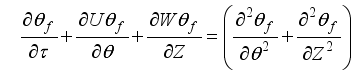 (13)
(13) 3.2. Mathematical Model
Figure 1. Geometry of the problem.
This is a representation of the problem setup and coordinate system. The bottom plate is maintained at 320 K, and the top plate is maintained at 298 K. The sidewalls are adiabatic, i.e., no heat transfer through them. Since Equations
11 and
13 are identical, they can be combined into one equation, as Mobedi, M
| [9] | Mobedi, M. (1994). A three-dimensional numerical study on natural convection heat transfer from rectangular fins on a horizontal surface. Doctoral dissertation, Middle East Technical University. |
[9]
.
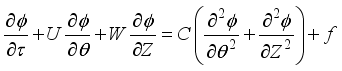 (14)
(14) Finite Difference Solution Method for Parabolic Differential Equations.
Equation
12 is reduced to;
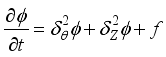 (15)
(15) Where
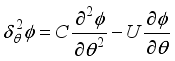 (16)
(16) 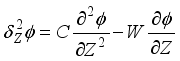 (17)
(17) There exist several finite difference methods for solving parabolic partial differential equations. Generally speaking, we can place these methods in three broad categories: the implicit, the explicit method, and Alternating Direction Implicit (ADI). For our study, we have used the explicit method.
So what is so special about the explicit method? Well, it moves from point to point through the dependent variable—node by node! But this method demands very small grid sizes or time steps in order to be stable. For that reason, it eventually demands an enormous amount of computer storage and a significant amount of time to compute.
Applying the explicit method to equation (
15) for any node (𝑖,) with a simple forward difference for the time term gives.
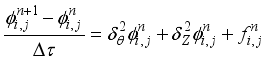 (18)
(18) 3.3. Thermal Boundary Conditions
The research includes heating of one wall at the base and cooling the upper portion of the opposing wall. Two thermal conditions were used:
1. Isothermal, which is represented by the equation Θ = Constant for vertical walls. The Dirichlet boundary condition, where Θhot = 1 and Θcold = 0, is applicable to both the hot and cold walls.
2. Adiabatic: The remaining walls temperatures were maintained at a steady level.
3.4. Velocity Boundary Conditions
There is no boundary condition for slippage. The air particles close to the surface will not follow the flow because the cohesive force is less than the adhesive force. Thus, there will be zero velocity on viscous fluid in relation to the wall at the solid boundary. As a result, the fluid's outermost molecules become adhered to the surface it runs over. At the surface, therefore, 𝑢 = 𝑣 = 𝑤 = 0. The boundary condition of free slide is applied. In this cylindrical enclosure, every restriction is assumed to be impenetrable. This implies that mass cannot pass through an impermeable solid surface as the velocity corresponding to the surface or boundary is zero.
4. Results and Discussion
4.1. Streamline Distribution
An imagined line in a fluid that indicates the direction of a fluid particle's velocity at a spot by the tan-gent at that point is called a streamline. The maximum value, 1.42 kg/s, was for the contours of the streamline for Rayleigh number
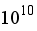
followed by 1.26 kg/s for the contours of the streamline for Rayleigh number
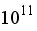
. The lowest value, 0.668 kg/s, is displayed by the contours of a streamline of Rayleigh number
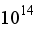
, and this value decreases as Rayleigh number increases, as displayed by the contours of a streamline of Rayleigh number
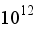
, which is 0.737 kg/s.
Figure 2 displays large vortices at both centers that take a circular trajectory that deforms with increasing in Rayleigh number. The flow is turbulent with a high Rayleigh number. The streamlines are chaotic, with numerous vortices, eddies, and complicated recirculation zones, rather than smooth again.
Physically, higher Rayleigh numbers cause stronger buoyancy forces, which drive the fluid motion more vigorously. This generates erratic streamline patterns distinguished by several vortices, eddies, and recirculation areas. Such flow behavior improves mixing and heat transfer, therefore improving thermal efficiency.
Figure 2 clearly shows this development: the initially round and organized vortices distort and finally become chaotic and turbid as the Rayleigh number rises.
4.2. Turbulence Intensity
Escalated of turbulence, or turbulence level, is the root-mean-square of cruel speed and turbulent speed variances. Contours of Rayleigh number
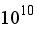
have a 70.3% turbulence; whereas streamline contours of Rayleigh number
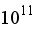
have 61.7% turbulence. Contours of Rayleigh number
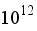
have medium intensity of turbulence, whereas contours of Rayleigh number
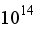
have low intensity of turbulence. The figures below show that as the Rayleigh number grows, the intensity of turbulence gets stronger. Further, there is more high turbulence in the direction of the heated wall. The flow becomes more unstable and the turbulence intensity increases as the Rayleigh number keeps on rising beyond the critical value. Larger turbulence intensity is a result of more random, fluctuating velocity fields and larger convection currents due to larger values of Ra.
This tendency implies that as the Rayleigh number increases, buoyancy-driven forces dominate over viscous forces, hence creating more strong convection currents and more dynamic flow instabilities physically. Such instabilities increase the degree of turbulence by generating larger and more regular velocity oscillations. The results show that the turbulence is not evenly distributed; instead, it is more severe near the heated lower wall where thermal gradients are strongest and buoyant plumes are most active.
This spatial distribution corresponds with physical expectations since the temperature difference raises heated fluid and generates complex turbulent interactions. Beyond the crucial Rayleigh number, the flow turns from an orderly convection pattern to fully evolved turbulence. Though greater turbulence intensity helps mixing and heat transfer, it also produces more complex and erratic flow behavior. The Rayleigh number is hence quite important for determining the spatial organization and intensity of turbulent flow within the cylindrical chamber as well as for triggering turbulence.
4.3 Contours of Effective Thermal Conductivity
In
Figure 10, maximum effective thermal conductivity is 17.531 (W/(m•K)), in
Figure 11, maximum effective thermal conductivity is 32 (W/(m•K)), in
Figure 12, effective thermal conductivity is 34.26 (W/(m•K)), and in
Figure 13, maximum effective thermal conductivity is 53.67 (W/(m•K)).
The Rayleigh number, which quantifies the flow of fluid due to buoyancy caused by temperature gradients, can alter the effective thermal conductivity of a fluid, like air. As the Rayleigh number increases, the fluid flow becomes more convective, which can influence its effective thermal conductivity.
At very high Rayleigh numbers, where convection is the dominant mechanism and the flow is turbulent, the effective thermal conductivity increases greatly. This is because the turbulent mixing increases the heat transfer, so that the effective thermal conductivity is higher than by conduction alone.
This movement on the physical level shows how buoyancy-driven convection is becoming more and more significant in transferring thermal energy. The fluid becomes more turbulent and the flow changes from laminar to turbulent as the Rayleigh number rises. Effectively serving as a thermal bridge, turbulent eddies and mixing improve the transfer of heat between warm and cold zones inside the container. This combination causes heat to be transferred more quickly than would be feasible just by molecular conduction.
At very high Rayleigh numbers, the turbulence intensifies, and large-scale chaotic flow structures develop, increasing the efficiency of energy transport. Consequently, the effective thermal conductivity greatly surpasses the material's own conduction value. This suggests that in turbulent natural convection, especially in cylindrical enclosures, convective heat transfer can control the total thermal performance.
5. Conclusion
1. Turbulence Intensity
Turbulence intensity also exhibits the same trend, with a maximum at Ra = 70.3% and a subsequent decrease to 61.7% at Ra =
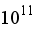
. At intermediate Rayleigh numbers Ra =
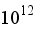
, turbulence is stabilized, and at extremely high Rayleigh numbers Ra =
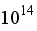
turbulence intensity is reduced, perhaps because of flow stabilization or transition to a more structured convection regime. Turbulence regions are densely packed near the hot wall, where intense buoyancy-driven currents generate random velocity fluctuations.
2. Streamline Distribution
The streamline distribution bears witness to the above observation in that the highest mass flow rate of 1.42 kg/s occurs when Ra =
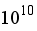
followed by 1.26 kg/s when Ra =
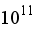
. For a higher value of the Rayleigh number, the mass flow rate will decrease to 0.668 kg/s when Ra =
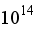
. At low Rayleigh numbers, flow is structured on the scale of large vortices, while at higher values of the Rayleigh number, the streamlines are turbulent with eddies and intricate zones of recirculation. Such a transition corresponds to the increasingly significant role played by turbulence and convective mixing.
3. Effective thermal conductivity
These results exhibit a definite trend: as the Rayleigh number increases, the effective thermal conductivity of the fluid (air) also increases significantly. The Rayleigh number is a quantification of the buoyancy-driven flow due to temperature gradients. At low Rayleigh numbers, conduction-dominated heat transfer prevails. However, with an increase in the Rayleigh number, convective heat transfer becomes more and more dominant.
At large enough Rayleigh numbers, convective turbulence enhances mixing of the fluid layers, dramatically increasing the effectiveness of heat transfer. The effective thermal conductivity is thus much greater than the one inferred on the basis of conduction alone. This helps to highlight the very important role played by buoyancy-driven convection in enhancing the thermal transport properties of fluid systems.
4. Overall Findings
These results confirm that Rayleigh number is a significant parameter governing heat transfer and fluid flow dynamics. At low Rayleigh numbers, conduction dominates, there is little turbulence, and streamlines are smooth. At larger Rayleigh numbers, convection dominates, turbulence is greater, the flow is disordered, turbulent eddies rather than ordered vortices, and heat transfer is greatly increased. At extremely high Rayleigh numbers, flow stabilization can suppress turbulence intensity even in the presence of vigorous convective motion.
This research highlights the significance of Rayleigh number in the optimization and design of natural convection systems wherein the turbulence streamlining, streamline dynamics and thermal conductivity have to be traded off in order to realize efficient heat transfer applications.
6. Validation of Results
1. Turbulence Intensity
Turbulence intensity increases with the Rayleigh number (Ra), reaching a peak value of around 70.3% at an intermediate Ra, after which it starts to decline. This trend indicates that as Ra grows, buoyancy-driven instability first boosts turbulence but that at really high Ra the flow changes to a more ordered or stabilized convection state, hence lowering random velocity oscillations. Awuor
| [14] | Awuor K. O. (2013). Turbulent natural convention in an enclosure: Numerical study of different models, Ph. D. Thesis, Kenyatta University, Kenya, 1-102. |
[14]
noted that the flow stays mostly laminar at low Rayleigh values. Turbulence gets worse as Ra rises, especially close to the heated wall where buoyancy forces are greatest. Beyond a particular limit, however, turbulence levels off or little diminishes as a result of flow stabilization or coordinated convection structures. Both investigations show non-monotonic behavior of turbulence intensity with initially increasing as a result of buoyancy-induced instability followed by a plateau or fall as the system moves to stabilized convection. This agreement supports the idea that, at high Ra, turbulence can be reduced even if thermal driving forces have been raised.
2. Streamline Distribution
At an ideal Rayleigh number, the mass flow rate peaks at 1.42 kg/s; as Ra grows further, it then drops to 0.668 kg/s. Analysis of streamlines reveals that flow changes from enormous, symmetric vortices at low Ra to complex recirculation regions and chaotic eddy creations at higher Ra values. At low Rayleigh numbers, Awuor & Gatitu
| [15] | Awuor, K. O. and Gatitu, M. (2017). Numerical simulation of natural convection in rectangular enclosures: International Journal for Innovative Research in Multidisciplinary Field. 3(7), 306-313. |
[15]
found symmetrical and stable vortices. With Ra above 10
10 the streamline patterns become chaotic, with vortex centers shifting and circulation velocities increasing, denoting strong convective mixing and turbulent flow. As Ra rises, both results show a definitive shift from structured to disordered flow. The mass flow rate peak and qualitative agreement in vortex behavior further support Ra's impact on convective dynamics.
3. Efficient Thermal Conductivity
Rising Ra results in a major increase in effective thermal conductivity caused by enhanced convective mixing. Conduction controls at low Ra; convection becomes more efficient as Ra rises, hence greatly improving thermal transport via turbulence. Awuor
| [14] | Awuor K. O. (2013). Turbulent natural convention in an enclosure: Numerical study of different models, Ph. D. Thesis, Kenyatta University, Kenya, 1-102. |
[14]
found that convection starts to dominate beyond Ra 10
10, with a sharp rise in the Nusselt number, a proxy for effective thermal conductivity. This suggests a transition from conduction-driven to convection-dominated heat transfer as Ra rises. Both studies affirm that higher Rayleigh numbers greatly increase thermal conductivity, mainly through better convective processes and turbulence.
7. Recommendations
Further research should be conducted in the following:
1. Determine the effect of altering the enclosure size with constant Rayleigh number on the isotherm and streamline distribution.
2. Determine how alterations in the fluid properties inside the enclosure affect the behavior of the system.
3. Determine the performance of the same enclosure when computed using other models, e.g., k-epsilon turbulence model.
Abbreviations
RANS | Reynolds-averaged Navier–stokes |
Ra | Rayleigh Number |
K | Kelvin |
ANSYS Fluent | Computational Fluid Dynamics (CFD) Software Tool |
Acknowledgments
We truly acknowledge the support of Jomo Kenyatta University of Agriculture and Technology (JKUAT) for its valuable resource, technical assistance, and invigorating academic environment. Their collaborative input was instrumental in the success of this research and is greatly valued by the entire team of researchers.
Author Contributions
Omariba Geofrey Ong'era: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Writing – original draft, Writing – review & editing
Johana Kibet Sigey: Conceptualization, Methodology, Supervision, Validation, Writing – review & editing
Jeconia Abonyo Okelo: Formal Analysis, Supervision, Validation, Visualization, Writing – review & editing
Stephen Mbugua Karanja: Conceptualization, Supervision, Writing – review & editing
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
Azzouz, R., & Ben Hamida, M. B. (2023). Unsteady natural convection heat transfer in a circular enclosure containing four heated cylinders under the influence of a magnetic field. Processes, 11(8), 2444.
|
| [2] |
Daiz, A., Hidki, R., Fares, R., & Charqui, Z. (2024). Finite element analysis of natural convection within a circular cavity containing a heated corrugated hollow cylinder. International Journal of Heat and Fluid Flow.
|
| [3] |
Enayati, H., Vafai, K., & Keblinski, P. (2016). Analysis of natural convection in cylindrical spaces used for crystal growth. Numerical Heat Transfer, Part A: Applications, 69(9), 963-981.
|
| [4] |
Gautam, M., Sharma, A., & Verma, R. (2022). Enhancing natural convection heat transfer in a cylindrical enclosure with an internal heat source. In Proceedings of the 12th International Conference on Advances in Thermal Engineering (pp. 435-448). Springer.
|
| [5] |
Ibrahim, M. N. J., Hammoodi, K. A., Abdulsahib, A. D., & Flayyih, M. A. (2022). Natural convection in an inclined nanofluid-filled cavity with hot inner bodies. International Journal of Heat and Technology, 40(3), 306-317.
|
| [6] |
Laidoudi, H. (2020). Effect of natural convection on heat transfer in a circular enclosure with multiple heated cylinders. Journal of Thermal Sciences and Engineering Applications, 12(4), 654-671.
|
| [7] |
Mahmood, M. A., Mustafa, M. A., Al-Azzawi, M. M., & Abdullah, A. R. (2024). Numerical investigation of natural convection heat transfer between two isothermal concentric vertical cylinders embedded with porous media. Journal of Fluid Mechanics and Thermal Sciences, 12(1), 45-63.
|
| [8] |
Medebber, M. A., Boumeddane, B., & Cherif, L. (2020). Transient free convection in a vertical cylindrical enclosure with adiabatic top and bottom walls. International Journal of Thermal Sciences, 156, 106460.
|
| [9] |
Mobedi, M. (1994). A three-dimensional numerical study on natural convection heat transfer from rectangular fins on a horizontal surface. Doctoral dissertation, Middle East Technical University.
|
| [10] |
Muia, M., & Kamau, P. (2018). Numerical modeling of turbulent natural convection in a rectangular enclosure. International Journal of Computational Fluid Dynamics, 32(5), 450-465.
|
| [11] |
Ong'era, O. G., Sigey, J. K., Okelo, J. A., Karanja, &S. M. (2021). Analysis of Turbulent Natural Convection with Localized Heating on the Ceiling and on the Floor and Cooling on Opposite Vertical Walls in a Rectangular Enclosure. International Journal of Science and Research (IJSR), 10(11), 523-529.
|
| [12] |
Shah, M., Ali, M., & Khan, S. (2024). Heat transfer enhancement in a vertical cylindrical cavity using phase-change materials and nanofluids. International Journal of Thermal Sciences, 200(3), 108425.
|
| [13] |
Zhou, Y., Xu, W., & Liang, X. (2024). Vortex-induced flow structures and their impact on natural convection heat transfer in a cylindrical enclosure. Journal of Heat Transfer, 146(1), 011101.
|
| [14] |
Awuor K. O. (2013). Turbulent natural convention in an enclosure: Numerical study of different models, Ph. D. Thesis, Kenyatta University, Kenya, 1-102.
|
| [15] |
Awuor, K. O. and Gatitu, M. (2017). Numerical simulation of natural convection in rectangular enclosures: International Journal for Innovative Research in Multidisciplinary Field. 3(7), 306-313.
|
Cite This Article
-
APA Style
Ong'era, O. G., Sigey, J. K., Okelo, J. A., Karanja, S. M. (2025). Mathematical Modelling of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. Applied and Computational Mathematics, 14(4), 183-192. https://doi.org/10.11648/j.acm.20251404.11
 Copy
|
Copy
|
 Download
Download
ACS Style
Ong'era, O. G.; Sigey, J. K.; Okelo, J. A.; Karanja, S. M. Mathematical Modelling of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. Appl. Comput. Math. 2025, 14(4), 183-192. doi: 10.11648/j.acm.20251404.11
 Copy
|
Copy
|
 Download
Download
AMA Style
Ong'era OG, Sigey JK, Okelo JA, Karanja SM. Mathematical Modelling of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder. Appl Comput Math. 2025;14(4):183-192. doi: 10.11648/j.acm.20251404.11
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.acm.20251404.11,
author = {Omariba Geofrey Ong'era and Johana Kibet Sigey and Jeconia Abonyo Okelo and Stephen Mbugua Karanja},
title = {Mathematical Modelling of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder
},
journal = {Applied and Computational Mathematics},
volume = {14},
number = {4},
pages = {183-192},
doi = {10.11648/j.acm.20251404.11},
url = {https://doi.org/10.11648/j.acm.20251404.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.acm.20251404.11},
abstract = {Turbulent natural convection in cylindrical enclosures is a significant phenomenon in most engineering and industrial applications, such as thermal insulation, electronics cooling, and building climate control. An explicit understanding of the transition of flow from laminar to turbulent and its influence on heat transfer is essential in terms of optimizing system performance. The study solves two major objectives: Model the governing equations of turbulent natural convection in a cylindrical enclosure using K-Omega turbulence model, and compute the effective thermal conductivity, turbulence intensity, and streamline distribution as functions of Rayleigh number. The enclosure that has been considered is an insulated vertical sidewall enclosure with a top wall at 298 K and a bottom wall at 320 K. The mathematical formulation consists of the Reynolds-Averaged Navier–Stokes (RANS) equations, the energy equation, and transport equations for turbulence, subject to the Boussinesq approximation to model buoyancy. A low-Reynolds-number two-equation model is used to model turbulence close to the walls, and the Prandtl number is set to 0.71 to model air as the working fluid. Numerical solutions are achieved by the use of the finite difference technique and verified by simulations done in ANSYS Fluent. The simulation identifies how structures flow and mechanisms of heat transfer change with increasing Rayleigh numbers. At small Rayleigh numbers, the flow is steady, conduction-dominated, with smooth streamlines and little or no turbulence. It is noted that as the Rayleigh number increases, buoyancy-driven convection becomes more significant, leading to the formation of vortices, intensified turbulence, and enhanced mixing, which collectively improve the effective thermal conductivity. The streamline distribution becomes increasingly complex and disordered, reflecting the transition to chaotic flow. These results demonstrate that the Rayleigh number is a key parameter influencing thermal and flow characteristics in cylindrical enclosures. The study provides practical insights in designing and optimizing systems involving buoyancy-induced turbulent heat transfer.},
year = {2025}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Mathematical Modelling of Turbulent Natural Convection of Heat Transfer with Localized Heating and Cooling on Opposite Surface of a Vertical Cylinder
AU - Omariba Geofrey Ong'era
AU - Johana Kibet Sigey
AU - Jeconia Abonyo Okelo
AU - Stephen Mbugua Karanja
Y1 - 2025/07/04
PY - 2025
N1 - https://doi.org/10.11648/j.acm.20251404.11
DO - 10.11648/j.acm.20251404.11
T2 - Applied and Computational Mathematics
JF - Applied and Computational Mathematics
JO - Applied and Computational Mathematics
SP - 183
EP - 192
PB - Science Publishing Group
SN - 2328-5613
UR - https://doi.org/10.11648/j.acm.20251404.11
AB - Turbulent natural convection in cylindrical enclosures is a significant phenomenon in most engineering and industrial applications, such as thermal insulation, electronics cooling, and building climate control. An explicit understanding of the transition of flow from laminar to turbulent and its influence on heat transfer is essential in terms of optimizing system performance. The study solves two major objectives: Model the governing equations of turbulent natural convection in a cylindrical enclosure using K-Omega turbulence model, and compute the effective thermal conductivity, turbulence intensity, and streamline distribution as functions of Rayleigh number. The enclosure that has been considered is an insulated vertical sidewall enclosure with a top wall at 298 K and a bottom wall at 320 K. The mathematical formulation consists of the Reynolds-Averaged Navier–Stokes (RANS) equations, the energy equation, and transport equations for turbulence, subject to the Boussinesq approximation to model buoyancy. A low-Reynolds-number two-equation model is used to model turbulence close to the walls, and the Prandtl number is set to 0.71 to model air as the working fluid. Numerical solutions are achieved by the use of the finite difference technique and verified by simulations done in ANSYS Fluent. The simulation identifies how structures flow and mechanisms of heat transfer change with increasing Rayleigh numbers. At small Rayleigh numbers, the flow is steady, conduction-dominated, with smooth streamlines and little or no turbulence. It is noted that as the Rayleigh number increases, buoyancy-driven convection becomes more significant, leading to the formation of vortices, intensified turbulence, and enhanced mixing, which collectively improve the effective thermal conductivity. The streamline distribution becomes increasingly complex and disordered, reflecting the transition to chaotic flow. These results demonstrate that the Rayleigh number is a key parameter influencing thermal and flow characteristics in cylindrical enclosures. The study provides practical insights in designing and optimizing systems involving buoyancy-induced turbulent heat transfer.
VL - 14
IS - 4
ER -
 Copy
|
Copy
|
 Download
Download
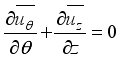 (1)
(1) 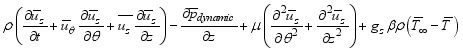 (2)
(2) 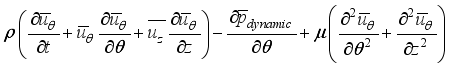 (3)
(3) 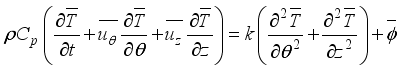 (4)
(4) 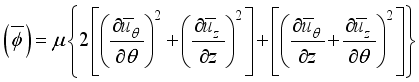
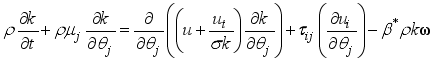 (5)
(5) 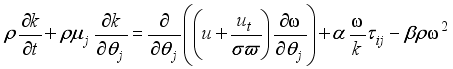 (6)
(6) 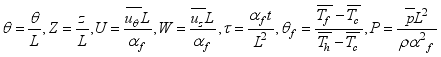 (7)
(7) 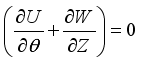 (8)
(8) 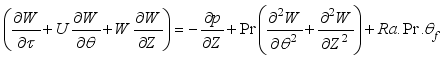 (9)
(9) 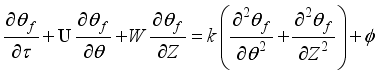 (10)
(10) 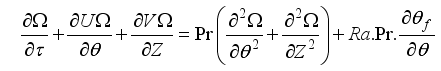 (11)
(11) 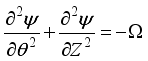 (12)
(12) 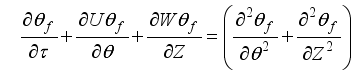 (13)
(13) 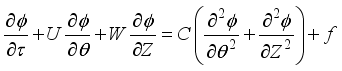 (14)
(14) 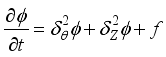 (15)
(15) 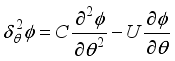 (16)
(16) 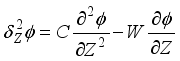 (17)
(17) 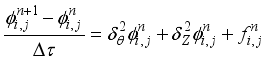 (18)
(18) 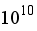 followed by 1.26 kg/s for the contours of the streamline for Rayleigh number
followed by 1.26 kg/s for the contours of the streamline for Rayleigh number 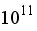 . The lowest value, 0.668 kg/s, is displayed by the contours of a streamline of Rayleigh number
. The lowest value, 0.668 kg/s, is displayed by the contours of a streamline of Rayleigh number 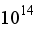 , and this value decreases as Rayleigh number increases, as displayed by the contours of a streamline of Rayleigh number
, and this value decreases as Rayleigh number increases, as displayed by the contours of a streamline of Rayleigh number 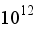 , which is 0.737 kg/s. Figure 2 displays large vortices at both centers that take a circular trajectory that deforms with increasing in Rayleigh number. The flow is turbulent with a high Rayleigh number. The streamlines are chaotic, with numerous vortices, eddies, and complicated recirculation zones, rather than smooth again.
, which is 0.737 kg/s. Figure 2 displays large vortices at both centers that take a circular trajectory that deforms with increasing in Rayleigh number. The flow is turbulent with a high Rayleigh number. The streamlines are chaotic, with numerous vortices, eddies, and complicated recirculation zones, rather than smooth again. 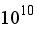 have a 70.3% turbulence; whereas streamline contours of Rayleigh number
have a 70.3% turbulence; whereas streamline contours of Rayleigh number 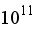 have 61.7% turbulence. Contours of Rayleigh number
have 61.7% turbulence. Contours of Rayleigh number 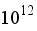 have medium intensity of turbulence, whereas contours of Rayleigh number
have medium intensity of turbulence, whereas contours of Rayleigh number 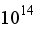 have low intensity of turbulence. The figures below show that as the Rayleigh number grows, the intensity of turbulence gets stronger. Further, there is more high turbulence in the direction of the heated wall. The flow becomes more unstable and the turbulence intensity increases as the Rayleigh number keeps on rising beyond the critical value. Larger turbulence intensity is a result of more random, fluctuating velocity fields and larger convection currents due to larger values of Ra.
have low intensity of turbulence. The figures below show that as the Rayleigh number grows, the intensity of turbulence gets stronger. Further, there is more high turbulence in the direction of the heated wall. The flow becomes more unstable and the turbulence intensity increases as the Rayleigh number keeps on rising beyond the critical value. Larger turbulence intensity is a result of more random, fluctuating velocity fields and larger convection currents due to larger values of Ra. 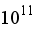 . At intermediate Rayleigh numbers Ra =
. At intermediate Rayleigh numbers Ra = 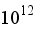 , turbulence is stabilized, and at extremely high Rayleigh numbers Ra =
, turbulence is stabilized, and at extremely high Rayleigh numbers Ra = 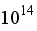 turbulence intensity is reduced, perhaps because of flow stabilization or transition to a more structured convection regime. Turbulence regions are densely packed near the hot wall, where intense buoyancy-driven currents generate random velocity fluctuations.
turbulence intensity is reduced, perhaps because of flow stabilization or transition to a more structured convection regime. Turbulence regions are densely packed near the hot wall, where intense buoyancy-driven currents generate random velocity fluctuations. 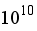 followed by 1.26 kg/s when Ra =
followed by 1.26 kg/s when Ra = 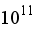 . For a higher value of the Rayleigh number, the mass flow rate will decrease to 0.668 kg/s when Ra =
. For a higher value of the Rayleigh number, the mass flow rate will decrease to 0.668 kg/s when Ra = 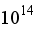 . At low Rayleigh numbers, flow is structured on the scale of large vortices, while at higher values of the Rayleigh number, the streamlines are turbulent with eddies and intricate zones of recirculation. Such a transition corresponds to the increasingly significant role played by turbulence and convective mixing.
. At low Rayleigh numbers, flow is structured on the scale of large vortices, while at higher values of the Rayleigh number, the streamlines are turbulent with eddies and intricate zones of recirculation. Such a transition corresponds to the increasingly significant role played by turbulence and convective mixing.