
A High Order Compact ADI Method for Solving 3D Unsteady Convection Diffusion Problems
Yongbin Ge,
Fei Zhao,
Jianying Wei
Issue:
Volume 7, Issue 1, February 2018
Pages:
1-10
Received:
3 December 2017
Accepted:
13 December 2017
Published:
12 January 2018
Abstract: In this paper, we develop a rational high order compact alternating direction implicit (RHOC ADI) method for solving the three dimensional (3D) unsteady convection diffusion equation. The present scheme, based on the idea of the fourth order rational compact finite difference operator for the spatial discretization and the Crank-Nicolson method for the time discretization, is fourth order accurate in space and second order accurate in time. The solution procedure consists of a number of tridiagonal matrix operations, which makes the computation to be cost-effective. It is shown by means of the discrete Fourier analysis that this method is unconditionally stable. Three test problems are given to demonstrate the performance of the present method. The numerical results show that the present RHOC ADI scheme has higher accuracy and better phase and amplitude error characteristics than the classical second order Douglas-Gunn ADI method [16] and some high order compact ADI methods including the Karaa’s HOC ADI method [26], Cao and Ge’s HOC ADI method [27], and our previous exponential HOC ADI method [28].
Abstract: In this paper, we develop a rational high order compact alternating direction implicit (RHOC ADI) method for solving the three dimensional (3D) unsteady convection diffusion equation. The present scheme, based on the idea of the fourth order rational compact finite difference operator for the spatial discretization and the Crank-Nicolson method for...
Show More

A Stable and Convergent Finite Difference Scheme for 2D Incompressible Nonlinear Viscoelastic Fluid Dynamics Problem
Issue:
Volume 7, Issue 1, February 2018
Pages:
11-18
Received:
4 December 2017
Accepted:
15 December 2017
Published:
12 January 2018
Abstract: In this study, a stable and convergent finite difference (FD) scheme based on staggered meshes for two-dimensional (2D) incompressible nonlinear viscoelastic fluid dynamics problem including the velocity vector field and the pressure field as well as the deformation tensor matrix is established in order to find numerical solutions for the problem. The stability, convergence, and errors of the FD solutions are analyzed. Some numerical experiments are presented to show that the FD scheme is feasible and efficient for simulating the phenomena of the velocity and the pressure as well as the deformation tensor in an estuary.
Abstract: In this study, a stable and convergent finite difference (FD) scheme based on staggered meshes for two-dimensional (2D) incompressible nonlinear viscoelastic fluid dynamics problem including the velocity vector field and the pressure field as well as the deformation tensor matrix is established in order to find numerical solutions for the problem. ...
Show More

A Reduced-Order Extrapolating Finite Difference Iterative Scheme for 2D Generalized Nonlinear Sine-Gordon Equation
Hong Xia,
Fei Teng,
Zhendong Luo
Issue:
Volume 7, Issue 1, February 2018
Pages:
19-25
Received:
17 December 2017
Accepted:
2 January 2018
Published:
18 January 2018
Abstract: In this study, a reduced-order extrapolating finite difference iterative (ROEFDI) scheme holding sufficiently high accuracy but containing very few degrees of freedom for the two-dimensional (2D) generalized nonlinear Sine-Gordon equation is built via the proper orthogonal decomposition. The stability and convergence of the ROEFDI solutions are analyzed. And the feasibility and effectiveness of the ROEFDI scheme are verified by numerical simulations. This means that the ROEFDI scheme is effective and feasible for finding the numerical solutions of the 2D generalized nonlinear Sine-Gordon equation.
Abstract: In this study, a reduced-order extrapolating finite difference iterative (ROEFDI) scheme holding sufficiently high accuracy but containing very few degrees of freedom for the two-dimensional (2D) generalized nonlinear Sine-Gordon equation is built via the proper orthogonal decomposition. The stability and convergence of the ROEFDI solutions are ana...
Show More

Topological Structure of Riesz Sequence Spaces
Merve Temizer Ersoy,
Bilal Altay,
Hasan Furkan
Issue:
Volume 7, Issue 1, February 2018
Pages:
26-30
Received:
29 December 2017
Accepted:
12 January 2018
Published:
20 January 2018
Abstract: In this paper, to be the Riesz matrix is symbolized by
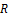
, it is defined the spaces
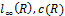
and
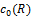
where for instance
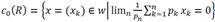
and computed its duals (
α-dual,
β-dual and
γ-dual). Furthermore, it is investigated topological structure of
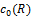
and determined necessary and sufficient conditions for a matrix
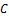
to map
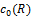
, or
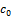
into
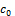
or
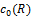
.



